Soal PAS Matematika Peminatan Kelas 10 [X] Kurikulum 2013 + Kunci Jawaban dan Pembahasannya

Berikut ini adalah soal latihan dalam menghadapi Penilaian Akhir Semester PAS atau Ulangan Akhir Semester UAS mata pelajaran Matematika Peminatan untuk kelas 10 [X] SMA/MA SMK/MAK Semester 1 Gasal/Ganjil Kurikulum 2013 Edisi Revisi 2017.

Soal-soal ini cocok digunakan sebagai bahan referensi dalam belajar untuk menghadapi ujian soal PAS/UAS Matematika Peminatan kelas X Semester 1 yang akan datang.

Bagi kalian yang masih merasa kesulitan dalam mengerjakan soal ini, maka diberikan pembahasannya sekaligus. Pembahasan berupa video pembelajaran daring/online mata pelajaran matematika SMA/MA.

Materi soal PAS Matematika Peminatan Kelas 10 Semester 1 diambil sesuai buku siswa/ buku guru Matematika Kelas 10 SMA/MA SMK/MAK Semester 1 Kurikulum 2013 edisi revisi 2017.

Soal terdiri dari 30 soal pilihan ganda. Materi dari soal PAS Matematika Peminatan Kelas 10 Semester 1 K-13 terdiri dari: 

1. Fungsi Eksponen 

2. Fungsi Logaritma

Soal PAS Matematika Peminatan Kelas 10 SMA/MA SMK/MAK Semester 1 Kurikulum 2013 

Jawablah soal di bawah ini dengan benar!

Nomor 1
Bentuk sederhana dari [5p^-3q⁴ : p⁵q^-3] × [5p²q² : p⁵q^-5]  adalah ....
A.  q¹¹/ 5p¹⁴
B.  5q¹⁴ / p¹¹
C.  5q¹⁴ / p¹¹
D.  5q¹⁴p¹¹
E.  5p¹⁴ / q¹¹

Nomor 2
Nilai dari [x²y^-1 + x³] / [3^-1z²] adalah ....

A. ⁷/₄

B. ⁴/₇

C. ²⁹/₁₆

D. ³/₇

E. ¹⁶/₂₈

Nomor 3

Nilai dari [2²⁰²³ + 2²⁰²¹] / [2²⁰²¹ – 2²⁰²⁰] adalah ....

A. 5

B. 10

C. 15

D. 20

E. 25

Nomor 4

Sebuah penampung air berbentuk balok dengan ukuran panjang 3,5 × 10³ m, lebar 2 × 10³ rn, dan kedaiaman 6 m. Akan disalurkan ke penampungan air yang lain, jika kecepatan air yang keluar melalui pipa 15 liter per menit, Berapa waktu yang dibutuhkan sehingga air di penampungan pertama habis ... menit. 

A. 2,8 × 10⁷

B. 3,8 × 10⁸  

C. 2,8 × 10⁹

D. 3 × 10⁹ 
E. 3,8 × 10⁹

Nomor 5

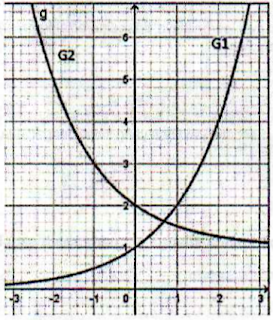
Perhatikan gambar berikut!

G₁ adalah grafik fungsi y = f(x) = 2^x, maka G₂ adalah garfik fungsi .... 

A. y = 2^x+2

B. y = 2^x + 2 

C. y = 2^-x + 2 

D. y = 2^-x + 1 

E. y = 2^-x 

Nomor 6
Grafik y = 16.2^x memotong graflk y = 2^-3x di titik yang berkoordinat .... 

A. [-1, 16] 

B. [-1, 8]

C. [1, 32]

D. [1, 16]

E. [4, 64]

Nomor 7
Kolera, penyakit yang menyerang usus, disebabkan oleh bakteri kolera yang berkembang biak secara eksponensial dengan membelah selnya dan dinyatakan dengan N = N₀.2^0,05t setiap jam. N adalah jumlah bakteri yang muncul setelah t jam dan N₀ adalah jumlah bakteri pada permulaan [t = 0]. Jika di awal terdapat 25 bakteri, banyak bakteri setelah 40 jam adalah .... 

A. 25  

B. 50  

C. 75

D. 100

E. 125

Nomor 8

Jika 3^x-2y = ¹/₈₁ dan 2^x-y – 16 = 0, maka nilal x + y = ....

A. 21 

B. 20 

C. 18

D. 16 

E. 14 

Nomor 9
Nilai-nilai x yang memenuhi persamaan [¼]^x-1 = ∛[2^3x-1] adalah ....

A. ²/₉
B. ⁹/₄

C. ⁵/₉

D. ⁷/₉

E. ⁴/₅

Nomor 10 
Himpunan penyelesaian dan persamaan eksponen 1000^{[x² – 3x – 4]} = 10^{[x² – 2x + 3]} adalah ....
A. {-³/₂, 5}

B. {-³/₂, -5}

C. {-³/₂, ⁷/₂}

D. {1, ⁷/₂}

E. {½, 9}

Nomor 11
Pak Hendra menabung uang di suatu bank sebesar Rp10.000.000,00 dengan bunga majemuk 10% per tahun. Jumlah tabungan Pak Hendra setelah 5 tahun adalah .... 

A. Rp10.000.000,00 [1 + 0,01]⁵  

B. Rp10.000.000,00 [1 + 0,1]⁵ 

C. Rp10.000.000,00 [1 + 0,1]⁴ 

D. Rp10.000.000,00 [1 + 0,01]⁴

E. Rp10.000.000,00 [1 + 0,01]⁸ 

Nomor 12
Himpunan penyelesaian dari persamaan eksponen 3^{x² + 3x – 10} = 5^{x² + 3x – 10} adalah .... 

A. {-5, -2} 

B. {-2, 5}  

C. {-5, 2}

D. {2, 2}

E. {2, 5}   

Nomor 13
Akar-akar persamaan 2² + 3.2^{x +2} + 32 = 0 adalah x₁ dan x₂. Jika x₁ > x₂. Maka nllai dari 2x₁ – x₂ adalah .... 

A. 2 

B. 4  

C. 6

D. 8 

E. 10
 

Nomor 14
Nilai x yang memenuhi pertidaksamaan ∛[1/27^2x] > [81^3x]/[3^18x-36] adalah ....

A. x > -18  

B. x > -9  

C. x > 9

D. x < 9

E. x < 18

Nomor 15 
Himpunan penyelesaian pertidaksamaan 4^{x² + x – 2}.2^{x² - 4x – 7} < ¹/₈ adalah .... 

A. {x | -⁴/₃ < x < 2} 

B. {x | -2 < x < ⁴/₃} 

C. {x | ⁴/₃ < x < 2}

D. {x | x < -2atau x > ⁴/₃} 

E. {x | x < -⁴/₃ atau x > 2}

PEMBAHASAN NO.1-15 ADA DISINI

Nomor 16
Jika ²log √[x² – 16] = 2, maka ^xlog 2 = ....

A. ⅕
B. ⅖

C. ⅗

D. ⅘

E. 4

Nomor 17 

Jika ⁴log 3 = p dan ³log 5 = q, maka ⁴log 15 = ....

A. [1+p] / pq

B. [1+q] / pq

C. pq / [1+p]

D. p[1+q]

E. q[1+p]

Nomor 18 

Jika a > 1, b> 1 dan c> 1, maka ^alog √3 × ^blog a⁴ × ³log √b = ....

A. ¼

B. ½ 
C. 1

D. 2

E. 3
 

Nomor 19

Jika $f(x)=\frac{^{7}\log x}{1-2.\, ^{7}\log x}$ maka nilai $f(x)+f(\frac{7}{x})=$ ....

A. -3 

B. -2 

C. -1

D. 0

E. 1

Nomor 20  

Energi yang dikeluarkan dalam suatu gempa bumi adalah 100.000 kj, untuk menghitung skala richter
menggunakan rumus R = ⅗ log K – 0,8. Jika R adalah skala Richter dan K adalah energi yang dikeluarkan. Maka nilai skala richter saat gempa terjadi adalah .... 

A. ²²/₁₀

B. ²⁸/₁₀

C. ⁴⁴/₁₀

D. ⁵³/₁₀

E. ⁶²/₁₀

Nomor 21  

Diketahui p = ¹²⁵log 625, q = ³²log 16 dan s = ²⁷log 81, nilai pq + qs = ....  

A. 32 

B. 15

C. ²⁰/₆

D. ¹⁶/₁₅ 

E. ³²/₁₅

Nomor 22  

Jika x₁ dan x₂ memenuhi persamaan ²log x^{[1+ ²log x]} = 2, maka nilai x₁ + x₂ = .....

A. 2¼

B. 2½

C. 4¼

D. 4½

E. 6¼

Nomor 23  

Jika log [3x + y] = 1 dan 3^y = [3^3x+2] / 81, maka nilai dari 5x + y = ....

A. 6 

B. 8

C. 10

D. 12 
E. 14 

Nomor 24 

Diketahui $f(x)$ =  ⁵log (5x – 15). Nilai dari $f(28)$ = .... 

A. 2  

B. 3 

C. 4

D. 5

E. 6 
 

Nomor 25
Misalkan intensitas bunyi $(I)$ pada percakapan normal adalah 10^-6 W/m². Taraf intensitas $(N)$ dalam desibel dinyatakan dengan $N(I)$ = 10 log $(I/I₀)$, dengan I₀ = 10^-12 W/m². Dalam hal ini, I₀ merupakan intensitas ambang pendengaran. Berapakah taraf intensitas dari percakapan normal tersebut? 

A. 30 dB  

B. 40 dB 

C. 50 dB

D. 60 dB 

E. 70 dB 

Nomor 26 

Penyelesaian dari persamaan 5^x = 3 adalah .... 

A. ³log 5

B. ¹⁵log 3 

C. ³log 10 

D. log 10

E. ⁵log 3

Nomor 27  

Penyelesaian dari persamaan ²log [x² + 4x – 4] = 3 adalah .... 

A. -6 atau -2 

B. -6 atau 2  

C. 3 atau-7

D. -5 atau 1 

E. -1 atau 5

Nomor 28
Penyelesaian dari persamaan logaritma ³log [x² + 5x – 23] =  ⁵log [x² + 5x – 23] adalah .... 

A. -6 atau 1
B. -4 atau 9
C. -9 atau 4
D. -7 atau 2
E. -8 atau 3

Nomor 29 

Batas-batas nilai yang memenuhi ⁵log [5x – 7] ≤ ⁵log [2x + 5] adalah ....

A. -⁵/₂ ≤ x ≤ 4

B. x ≥ -⁵/₂

C. ⁷/₅ ≤ x ≤ 4

D. x ≤ -⁵/₂ atau x ≥ 4

E.  x ≤ ⁷/₅ atau x ≥ 4

Nomor 30
Nilai x yang memenuhi pertidaksamaan ^⅓log [x+5] ≤ ^⅓log [3x–7] adalah ....

A. x ≥ 6

B. x ≥ -5

C. x ≥ ⁷/₃

D. ⁷/₃ ≤ x ≤ 6 

E. -5 ≤ x ≤ 6

PEMBAHASAN NO.16-30 ADA DISINI

SELAMAT BELAJAR

===

Soal latihan persiapan tes/ujian/ulangan PH/UH PTS/UTS PAS/UAS PAT/UKK USBN UNBK

Video pembelajaran materi dan soal Matematika Wajib/Peminatan Kelas 10, 11, 12 SMA/MA SMK/MAK.