Rangkuman Materi TRANSFORMASI GEOMETRI dan Pembahasan Soal-soalnya - Matematika Kelas 9 IX Kurikulum 2013 Revisi 2018

3.1 Pencerminan [Refleksi]

Kegiatan 1 Pencerninan Suatu Benda

Refleksi atau pencerminan merupakan salah satu jenis transformasi yang memindahkan setiap titik pada suatu bidang [atau bangun geometri] dengan menggunakan sifat benda dan bayangannya pada cermin datar.

Sifat bayangan benda yang dibentuk oleh pencerminan di antaranya sebagai berikut.

Bayangan suatu bangun yang dicerminkan memiliki bentuk dan ukuran yang sama dengan bangun aslinya.
Jarak bayangan ke cermin sama dengan jarak benda aslinya ke cermin.
Bayangan bangun pada cermin saling berhadapan dengan bangun aslinya

Gambar di bawah ini merupakan contoh pencerminan [refleksi] dari segi empat PQRS terhadap garis α sehingga menghasilkan bayangan yaitu segi empat P’Q’R’S’.

Berikut ini merupakan langkah-langkah untuk menggambar bayangan hasil refleksi segi empat PQRS terhadap garis α.

Langkah 1

Gambar ruas garis yang tegak lurus terhadap garis α dari P, Q, R, dan S.

Langkah 2

Tentukan titik P’, Q’, R’, dan S’ sehingga garis α tegak lurus dan membagi PP’, QQ’, RR’, dan SS’ sama panjang. Titik P’, Q’, R’, dan S’ merupakan bayangan titik P, Q, R, dan S.

Langkah 3

Hubungkan titik-titik P’, Q’, R’, dan S’. Oleh karena P’, Q’, R’, dan S’ merupakan bayangan dari P, Q, R, dan S yang direfleksikan oleh garis α, maka segi empat P’Q’R’S’ merupakan bayangan segi empat PQRS.

Materi Esensi Pencerminan [Refleksi]

Refleksi atau pencerminan merupakan satu jenis transformasi yang memindahkan setiap titik pada suatu bidang dengan mengggunakan sifat bayangan cermin dari titiktitik yang dipindahkan. Perhatikan gambar di bawah.

Gambar di samping menunjukkan contoh refleksi (pencerminan) bangun datar ABCDE pada garis m. Perhatikan bahwa ruas garis yang menghubungkan titik dan bayangannya tegak lurus terhadap garis m. Garis m disebut garis refleksi untuk ABCDE dan bayangannya A’B’C’D’E’.

Karena E terletak pada garis refleksi, titik awal dan bayangannya berada di titik yang sama. Jarak antara A terhadap garis m sama dengan jarak A’ terhadap garis m, begitu pula untuk titik sudut yang lainnya dan bayangannya yang memiliki jarak sama terhadap garis refleksi m.

Jika diketahui sebarang titik dengan koordinat [x, y] pada koordinat kartesius, maka koordinat bayangan hasil pencerminannya dapat dilihat pada Tabel 3.4 berikut ini.

LIHAT PENJELASAN MATERI PENCERMINAN (REFLEKSI)

Latihan 3.1 Pencerminan [Refleksi]

1. Tunjukkan apakah gambar yang berwarna biru merupakan hasil pencerminan dari gambar yang berwarna merah. Berikan penjelasanmu.

2. Tentukan berapa banyak simetri lipat yang dimiliki gambar berikut.

3. Gambar masing-masing bangun berikut dan bayangannya terhadap refleksi yang diberikan.

a. Segi empat JKLM dengan titik sudutnya di J [2, 2], K [7, 4], L [9, –2], dan M [3, –1] terhadap sumbu-y.

b. Trapesium dengan titik sudutnya di D [4, 0], E [–2, 4], F [–2, –1], dan G [4, –3] terhadap titik asal.

c. ∆ABC dengan titik sudutnya di A [4, –2], B [4, 2], dan C [6, –2] terhadap garis y = x.

d. ∆OPQ dengan titik sudutnya di O [–2, 1], P [0, 3], dan Q [2, 2] terhadap garis y = –x.

e. Segi empat WXYZ dengan titik sudutnya di W [2, –1], X [5, –2], Y [5, –5], dan Z [2, –4] terhadap garis y = 2.

4. Cerminkan segitiga DEF terhadap garis y = x. Gambar segitiga D’E’F’ dan tuliskan koordinatnya yang merupakan hasil pencerminan DEF terhadap garis y = x.

5. Huruf mana yang akan tetap sama jika dicerminkan terhadap suatu garis?

6. Segi empat KLMN dengan titik sudut di K [–2, 4], L [3, 7], M [4, –8], dan N [–3, –5] direfleksikan terhadap sumbu-x kemudian direfleksikan terhadap garis y = x. Tentukan koordinat K’’L’’M’’N’’.

7. Segitiga HIJ direfleksikan terhadap sumbu-x, kemudian sumbu-y, kemudian titik asal. Hasilnya refleksinya berkoordinat di H’’’[2, 3], I’’’[8, –4], dan J’’’[–6, –7]. Tentukan koordinat H, I, dan J.

PEMBAHASAN LENGKAP LATIHAN 3.1 (REFLEKSI)

3.2 Pergeseran [Translasi]

Materi Esensi Pergeseran [Translasi]

Translasi merupakan salah satu jenis transformasi yang bertujuan untuk memindahkan semua titik suatu bangun dengan jarak dan arah yang sama.

Translasi pada bidang Kartesius dapat dilukis jika kamu mengetahui arah dan seberapa jauh gambar bergerak secara mendatar dan atau vertikal. Untuk nilai yang sudah ditentukan a dan b yakni translasi [a b] memindah setiap titik P[x, y] dari sebuah bangun pada bidang datar ke P’[x + a, y + b]. Translasi dapat disimbolkan dengan [x, y] → [x + a, y + b].

LIHAT PENJELASAN MATERI PERGESERAN [TRANSLASI]

Latihan 3.2 Pergeseran [Translasi]

1. Tentukan apakah gambar yang berwrna biru merupakan hasil pergeseran dari gambar yang berwarna merah. Berikan penjelasanmu.

2. Gambar dan tentukan koordinat hasil translasi dari bangun datar di bawah ini.

a. Translasikan segi empat merah sejauh 2 satuan ke kiri dan 5 satuan ke bawah

b. Translasikan segitiga merah sejauh 3 satuan ke kanan dan 4 satuan ke bawah.

3. Segitiga FGH ditranslasi sehingga menghasilkan bayangan ∆PQR. Diketahui koordinat F [3, 9], G [–1, 4], P [4, 2], dan R [6, –3], tentukan koordinat H dan Q. Tentukan pula translasinya.

4. Segitiga WAN berkoordinat di W [0, 1], A [1, –2] dan N [–2, 1]. Gambarlah segitiga tersebut beserta bayangannya setelah translasi:

a. 1 satuan ke kiri dan 5 satuan ke atas

b. [x + 2, y + 4]

c. 3 satuan ke kanan dan 3 satuan ke bawah

d. kemudian dicerminkan terhadap sumbu-y.

5. Jelaskan translasi yang menggerakkan bangun datar yang berwarna biru menjadi bangun datar yang berwarna merah.

6. Diketahui Segitiga OPQ berkoordinat di O [2, 5], P [–3, 4], dan Q [4, –2] ditranslasikan sehingga didapatkan koordinat bayangannya adalah O’ di [3, 1]. Tentukan pasangan bilangan translasinya dan koordinat titik P’ dan Q’.

7. Seekor harimau sedang berburu rusa di dalam hutan. Berdasarkan hasil pemantauan diketahui bahwa koordinat rusa berada di titik A dan koordinat harimau berada pada titik B. Rusa tersebut kemudian bergerak menuju titik C.

a. Tentukan pasangan bilangan translasi yang menggerakkan rusa dari titik A menuju titik C.

b. Jika harimau menggunakan translasi yang sama dengan yang dilakukan oleh rusa, apakah harimau dapat menangkap rusa tersebut?

c. Tentukan pasangan bilangan translasi yang harus dilakukan oleh harimau agar ia mendapatkan rusa.

PEMBAHASAN LATIHAN 3.2 PERGESERAN (TRANSLASI)

3.3 Perputaran [Rotasi]

Materi Esensi Perputaran [Rotasi]

Rotasi merupakan salah satu bentuk transformasi yang memutar setiap titik pada gambar sampai sudut dan arah tertentu terhadap titik yang tetap. Titik tetap ini disebut pusat rotasi. Besarnya sudut dari bayangan benda terhadap posisi awal disebut dengan sudut rotasi.

Gambar di bawah ini menunjukkan rotasi bangun ABCD terhadap pusat rotasi, R. Besar sudut ARA’, BRB’, CRC’, dan DRD’ sama. Sebarang titik P pada bangun ABCD memiliki bayangan P’ di A’B’C’D’ sedemikian sehingga besar ∠PRP’ konstan. Sudut ini disebut sudut rotasi.

Suatu rotasi ditentukan oleh arah rotasi. Jika berlawanan arah dengan arah perputaran jarum jam, maka sudut putarnya positif. Jika searah perputaran jarum jam, maka sudut putarnya negatif. Pada rotasi, bangun awal selalu kongruen dengan bayangannya.

LIHAT PENJELASAN MATERI PERPUTARAN [ROTASI]

Latihan 3.3 Perputaran [Rotasi]

1. Jelaskan apakah gambar yang berwarna biru merupakan hasil rotasi dari gambar yang berwarna merah. Jika ya, dapatkan berapa besar sudut rotasi dan bagaimana arah dari rotasi tersebut.

2. Segi empat PQRS berkoordinat di P [2, –2], Q [4, –1], R [4, –3] dan S [2, –4]. Gambarlah bayangan PQRS pada rotasi 90⁰ berlawanan arah jarum jam yang berpusat di titik asal.

3. Salinlah ∆WAN berikut. Kemudian rotasikan segitiga tersebut sebesar 90⁰ searah jarum jam yang berpusat di titik H.

4. Gambar bayangan rotasi setiap bangun berikut dengan sudut 90⁰ jika diketahui arah dan pusat rotasi. Tentukan koordinat titik-titik bayangannya. ∆WAN dengan W [–4, 1], A [–2, 1], dan N [–4, –3] berlawanan arah jarum jam dengan pusat rotasi di titik N.

5. Gambar bayangan tranformasi untuk setiap segitiga berikut dengan mencerminkan segitiga pada garis yang diketahui. Bayangan akhir dari setiap bangun juga merupakan hasil rotasi. Tentukan koordinat bayangan dan sudut rotasi.

a. ∆TUV dengan T [4, 0], U [2, 3], dan V [1, 2] direfleksikan pada sumbu-y dilanjutkan sumbu-x.

b. ∆KLM dengan K [5, 0], L [2, 4], dan M [–2, 4] direfleksikan pada garis y = x dilanjutkan sumbu-x.

c. ∆XYZ dengan X [5, 0], Y [3, 4], dan Z [–3, 4] direfleksikan pada garis y = –x dilanjutkan garis y = x.

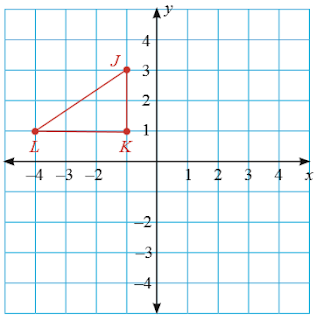
6. Diketahui segitiga JKL seperti pada gambar di bawah ini.

a. Rotasikan segitiga JKL dengan sudut rotasi 90⁰ searah jarum jam dengan pusat rotasi titik asal [0, 0]. Berapakah koordinat titik sudut dari segitiga J’K’L’ yang merupakan bayangan dari segitiga JKL?

b. Rotasikan segitiga JKL dengan sudut rotasi 180⁰ searah jarum jam dengan pusat rotasi titik asal [0, 0]. Berapakah koordinat titik sudut dari segitiga J’K’L’ yang merupakan bayangan dari segitiga JKL?

7. Diketahui segitiga RST dengan koordinat titik sudut di R[3 ,6], S[–5, 2] dan T[3, –3]. Gambar bayangan hasil transformasinya jika diketahui segitiga tersebut:

a. Dirotasi 90⁰ searah jarum jam yang berpusat di titik asal kemudian dicerminkan terhadap sumbu-y.

b. Dirotasi 90⁰ berlawanan arah jarum jam yang berpusat di titik asal kemudian didilatasi dengan faktor skala 2 berpusat di titik asal.

c. Dirotasi 180⁰ berlawanan arah jarum jam yang berpusat di titik asal kemudian

diitranslasi [a b] setelah itu dicerminkan terhadap sumbu-x.

PEMBAHASAN LATIHAN 3.3 PENCERMINAN [ROTASI]

3.4 Dilatasi

Materi Esensi Dilatasi

Dilatasi terhadap titik pusat merupakan perkalian dari koordinat tiap-tiap titik pada suatu bangun datar dengan faktor skala sebesar k. Faktor skala menentukan apakah suatu dilatasi merupakan pembesaran atau pengecilan. Secara umum dilatasi dari suatu koordinat [x, y] dengan faktor skala k akan menghasilkan koordinat [kx, ky] atau dapat ditulis [x, y] → (kx, ky). Ketika k > 1 maka dilatasi tersebut termasuk ke dalam pembesaran, tetapi jika 0 < k < 1 maka dilatasi tersebut termasuk ke dalam pengecilan. Untuk memperbesar atau memperkecil bangun, letak pusat dilatasi dapat di dalam, di luar, atau pada tepi bangun yang akan didilatasikan.

LIHAT PENJELASAN MATERI DILATASI

Latihan 3.4 Dilatasi

1. Tunjukkan apakah gambar yang berwarna biru merupakan hasil dilatasi dari gambar yang berwarna merah. Berikan penjelasanmu.

2. Gambar yang berwarna biru merupakan hasil dilatasi dari gambar berwarna merah. Tentukan faktor skala dan jenis dilatasinya.

3. Titik sudut dari masing-masing bidang datar diberikan sebagai berikut. Gambar bidang datar yang dimaksud dan bayangannya setelah dilatasi dengan faktor skala yang diberikan masing-masing. Sebutkan jenis dilatasinya.

a. A [1, 1], B [1, 4], dan C [3, 1] dengan faktor skala 4

b. G [–2, –2], H [–2, 6], dan J [2, 6] dengan faktor skala 0,25

c. Q [–3, 0], R [–3, 6], S [4, 6], dan T [4, 0] dengan faktor skala 1/3

4. Garis TU berkoordinat di T [4, 2] dan U [0, 5]. Setelah didilatasi, bayangan yang terbentuk memiliki koordinat di T’ [6, 3] dan U’ [12, 11]. Tentukan faktor skala yang digunakan.

5. Segitiga KLM berkoordinat di K[12, 4], L[4, 8], dan M[8, –8]. Setelah dua kali dilatasi berturut-turut yang berpusat di titik pusat dengan faktor skala yang sama, bayangan akhirnya memiliki koordinat K’’[3, 1], L’’[1, 2], dan M’’[2, –2]. Tentukan faktor skala k yang digunakan untuk dilatasi ∆KLM menjadi ∆K’’L’’M’’.

6. Gambar sebarang persegi pada bidang koordinat [kamu bebas menentukan panjang sisi dari persegi tersebut]. Pilih faktor skala 2, 3, 4, dan 5 kemudian dilatasikan persegi yang telah gambar dengan masing-masing faktor skala tersebut. Gambar bayangan hasil dilatasi dengan masing-masing faktor skala. Hitung luas tiap-tiap persegi, baik persegi awal, maupun persegi hasil dilatasi dengan masing-masing faktor skala.

a. Berapa kali lebih besar luas persegi hasil dilatasi dengan menggunakan masing-masing faktor skala jika dibandingkan dengan luas persegi awal?

b. Bagaimana rumus untuk mementukan luas persegi hasil dilatasi jika diketahui panjang sisi dari persegi awal adalah r dan faktor skala k? [Dapatkan rumus tersebut tanpa harus menggambar bayangan hasil dilatasi, gunakan perbandingan pada jawaban a]

c. Jika diberikan panjang sisi persegi awal 4 satuan, dan faktor skala 7. Berapa kali lebih besar luas persegi hasil dilatasi jika dibandingkan dengan luas persegi awal?

7. Gunakan lampu senter dan tanganmu untuk membuat bayangan kelinci pada dinding.

a. Menurutmu mana yang lebih besar, apakah tanganmu yang asli atau bayangan tanganmu yang membentuk gambar kelinci?

b. Jika dihubungkan dengan dilatasi, merepresentasikan apakah lampu senter yang digunakan pada percobaan tersebut?

c. Berdasarkan hasil perhitungan diketahui bahwa panjang hari tangan 7 cm, sedangkan panjang bayangannya di dinding 14 cm. Berapakah faktor skalanya?

d. Jika tanganmu digerakkan mendekati lampu senter, menurutmu apa yang akan terjadi pada bayangannya di dinding? Apa hubungannya dengan faktor skala?

8. Diketahui segitiga ABC dengan koordinat titik sudut di A [6, 12], B [–9, 3] dan C [6, –6]. Gambar bayangan hasil transformasinya jika diketahui segitiga tersebut:

a. Didilatasi dengan menggunakan faktor skala 1 3 dengan pusat titik asal kemudian dirotasi 90⁰ searah jarum jam yang berpusat di titik asal.

b. Didilatasi dengan menggunakan faktor skala 2 dengan pusat titik asal kemudian diitranslasi setelah itu dicerminkan terhadap sumbu-y

PEMBAHASAN LATIHAN 3.4 DILATASI

[Sebagian pembahasan masih dalam proses]

====

Sumber: Buku Siswa Matematika/ Kementerian Pendidikan dan Kebudayaan. Edisi Revisi 2018. Jakarta: Kementerian Pendidikan dan Kebudayaan.

Fastest-Math